0013-A-Eulersche Knickfälle
Casimir Katz | Casimir Katz | Roland Sauer | Walter RustlerA0 Classification
| Class | Analytical Verification Example |
|---|---|
| Type of structure | Framework |
| Mechanics | Statics-Stability Problem |
| Material law | Elastic |
| Building material | General |
| Design type | Stability Analysis |
| Design code | keine Norm |
| Status |
published on 23-04-2018 and qualified on 13-06-2018 |
A1 Problem description
Von Leonhard Euler stammen die wohlbekannten Stabilitätsfälle I bis IV für zentrisch gedrückte Stäbe.
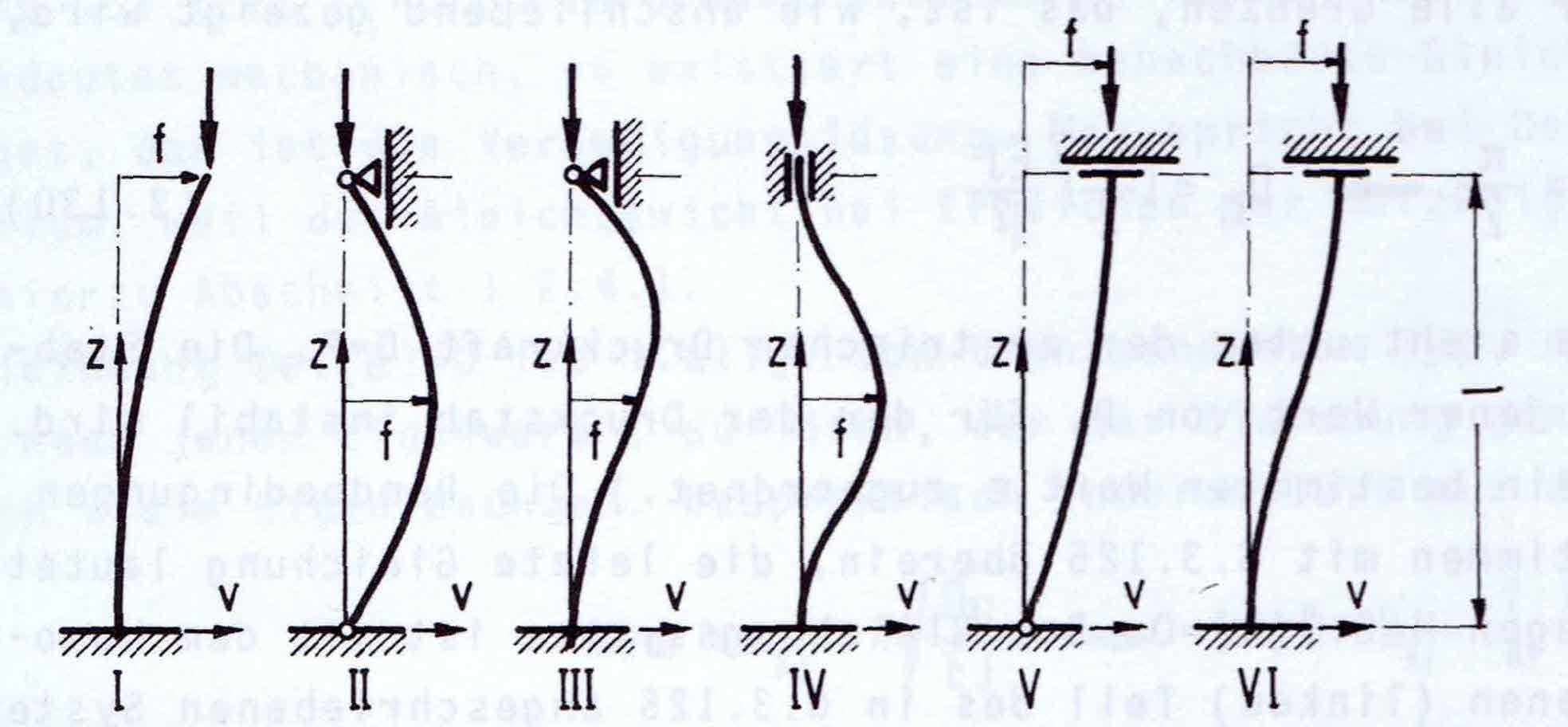
Den Lösungen der Differentialgleichungen liegen trigonometrische Funktionen zu Grunde, die von einem klassischen finiten Stabelement mit Polynomen nicht exakt abgebildet werden können. Zur Bewertung des Elementansatzes ist es daher erforderlich die Ergebnisse auch mit einer groben Elementeinteilung zu ermitteln.
Bei den meisten FE-Programmen werden außerdem per Voreinstellung Schubverformungen mit angesetzt, die bei schlanken Stützen zwar nur einen geringen Einfluss haben, aber ebenfalls verhindern, dass man die exakten theoretischen Werte trifft.
Als dritter Punkt sei vermerkt, dass bei der Beschreibung von Stabgelenken häufig eine sogenannte "statische" Kondemsation angewendet wird, die weder für dynamische noch Stablilitätseigenformen zutreffende Lösungen erlaubt.
Als System zur numerischen Evaluation soll ein Querschnitt HEB 300 mit einem Iy von 25170 cm4 und einem E-Modul von 210000 MPa sowie einer Systemlänge L = 16000 mm verwendet werden.
A5 References
[1] Ch. Petersen, Statik und Stabilität der Baukonstruktionen, Vieweg, 1980.
[2] F. Hartmann, C. Katz, Structural Analysis with Finite Elements, Springer, 2007, 2. ed..
[3] F. Gruttmann, R. Sauer, W. Wagner, A geometrical nonlinear eccentric 3D-beam element with arbitrary cross-sections, in: Computer Methods in Applied Mechanics and Engineering 160 (1998), 383-400.
Edit References
Delete?
Are you sure you want to delete this