0038-D-DBV-AK Software-Spannbetonbinder mit sofortigem Verbund nach DIN EN 1992-1-1 mit NA, Teil 2: Nachweis der Kippstabilität
Walter Pauli | Walter Pauli | David Krybus | Jürgen BellmannD0 Klassifikation
| Klasse | Normenbasiertes Verifikationsbeispiel |
|---|---|
| Tragwerkstyp | räumliches Tragwerk, Stabtragwerk-Balken |
| Mechanik | Statik-Theorie II. Ordnung, Statik-geometrisch nichtlinear |
| Materialgesetz | multilinear-elastisch |
| Baustoff | Beton, Stahlbeton, Spannbeton |
| Nachweisformat | Schnittgrößenermittlung, Stabilitätsnachweis, Tragfähigkeitsnachweis (GZT) |
| Norm | DIN EN 1992 |
| Status |
veröffentlicht am 28.03.2022 |
D1 Problembeschreibung
1.1 Aufgabenstellung
Für einen im Spannbett vorgespannten Dachbinder wird der Kippnachweis im Grenzzustand der Tragfähigkeit GZT geführt. Grundlage des Nachweises ist DIN EN 1992-1-1 mit dem nationalen Anhang DIN EN 1992-1-1/NA.
Das Beispiel ist in [1] ausführlich behandelt und stellt eine Fortsetzung zu dem Beispiel 0031-D-DBV-AK Software-Spannbetonbinder mit sofortigen Verbund nach DIN EN 1992-1-1 mit NA dar. Die Systemangaben und die Belastungen sind identisch, wobei sich das Beispiel hier auf den Nachweis der Kippstabilität konzentriert.
1.2 Theoretische Grundlagen
Der Nachweis erfolgt am verformten System mit einer geometrisch und physikalisch nichtlinearen Berechnung. Folgende Effekte werden berücksichtig:
- geometrische Imperfektionen und Kriechverformungen
- Lasteinleitung der Dachlasten am Obergurt
- Verdrehungen um den Schubmittelpunkt
- reduzierte Biege- und Torsionssteifigkeit infolge Rissbildung
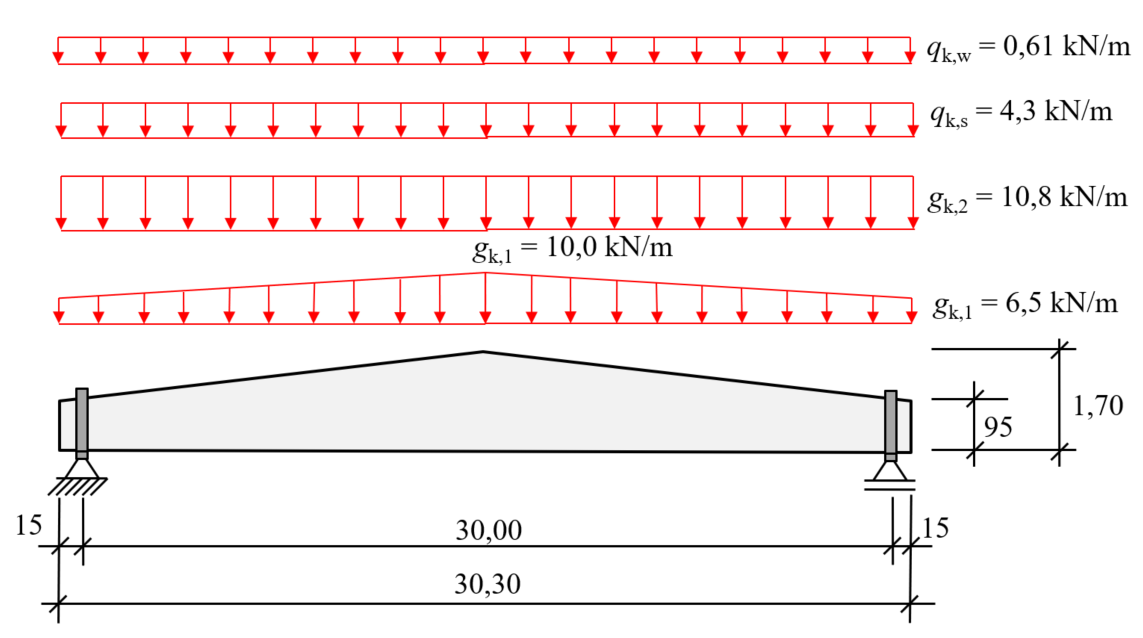
1.3 System
- Spannweite: L0 = 30.00 m
- Trägerlänge: Lges = 30.30 m
- Trägerhöhe am Auflager: h0 = 0.95 m
- Trägerhöhe in Feldmitte: hm = 1.70 m
- Montageanker ab Trägeranfang/ende: LM = 3.75 m
- Transport Trägeranfang/ende: Lli = 2.00 m, Lre = 5.50 m
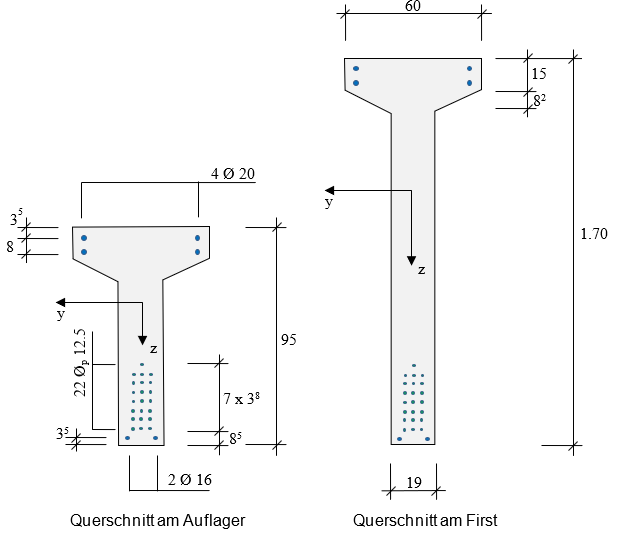
1.4 Querschnitte
1.5 Material
Beton
- C 50/60
- Zement Klasse R
- reduzierter Teilsicherheitsbeiwert γc = 1.35
Die Materialsicherheit des Betons wird mit γc = 1.35 gemäß DIN EN 1992-1-1/NA, NDP zu A.2.3 angesetzt.
Dies setzt voraus, dass bei einer werksmäßigen und ständig überwachten Herstellung durch eine Überprüfung der
Betonfestigkeit an jedem Fertigteil sichergestellt wird, dass alle Fertigteile mit zu geringer Festigkeit ausgesondert werden.
Zusätzlich wird davon ausgegangen, dass neben der Betondruckfestigkeit auch der Elastizitätsmodul des Betons
einer Qualitätskontrolle unterliegt und für Ecm ebenfalls die Sicherheit auf γcE = 1.35 reduziert werden kann.
Betonstahl
- B 500B
Spannstahl
- St 1570/1770
- 7-Draht Litze, sehr niedrige Relaxation
- Wärmebehandlung im Spannbett: T = 60° C
- Nenndurchmesser Litze: ϕp = 12.5 mm
- Nennquerschnitt je Litze: Ap = 0.93 mm2
- Vorspannung je Litze: σp,0(0) = 1000 N/mm2
- sofortige Verluste infolge Kurzeitrelaxation 4 %
1.6 Randbedingungen für Kriechen, Schwinden und Relaxation
Lagerung:
- Lösen der Verankerung nach t0 = 1 Tag, schrittweises Absetzen der Spannkraft
zul σc(t) = 0.7 fck(t0) wird vom Fertigteilhersteller garantiert - 50 % relative Luftfeuchtigkeit während der Lagerung
Transport und Montage:
- Transport des Binders nach tT = 10 Tage
- Montage des Binders nach tM = 11 Tage
Nutzung:
- Aufbringen der Zusatzlasten nach t1 = 21 Tage
- Innenbauteil mit 50 % relativer Luftfeuchte
- Expositionsklasse XC1
1.7 Bewehrung
Betonstahl:
- Obergurt: 4 ø 20 = 12.56 cm2, Achsabstand d1 = 35 mm
- Untergurt: 2 ø 16 = 4.02 cm2, Achsabstand d1 = 35 mm
Spannstahl:
- 22 Litzen = 20.45 cm2, Abstand zum unteren Rand d1 = 85 mm, untereinander 38 mm
1.8 Einwirkungen
- Eigengewicht Trägeranfang/ende: gk,a = 6.5 kN/m, Trägermitte: gk,m = 10.0 kN/m
- zusätzliches Eigengewicht: Δgk = 10.8 kN/m
- Schnee: qk,s = 4.3 kN/m
- Winddruck: qk,w = 0.61 kN/m
- Wind horizontal: qk,wh = 0.33 kN/m
Als Lastangriffspunkt wird für das zusätzliche Eigengewicht, den Schnee und den Winddruck der Obergurt des Binders angesetzt. Das Eigenwicht und die horizontale Windlast greifen in der Schwerachse an. Die horizontale Windlast ist in dem fertig gestellten System nicht mehr vorhanden.
1.9 Imperfektionen
- ungewollte Imperfektionen ei = l/300 = 100 mm gemäß DIN EN 1992-1-1, 5.9
- zusätzlich ist der Kriecheinfluss zu berücksichtigen
die Kriechzahl für den Zeitabschnitt nach der Montage darf mit φ(t1,∞) = 1.56 angenommen werden
Die Imperfektionen sind als seitliche Auslenkung mit einem parabolischen oder sinusförmigen Verlauf anzusetzen.
Alternativ kann nach [2] eine Vorverformung von l/500 zuzüglich einer Querschnittsverdrehung von 0.75 % angesetzt werden. Der Einfluss des Kriechens ist zusätzlich zu berücksichtigen. Dieser Ansatz wird hier jedoch nicht weiterverfolgt.
1.10 Nachweis der Kippstabilität
Der Nachweis der Kippstabilität ist für vier Zeitpunkte zu führen.
| Zeitpunkt [Tage] |
Lagerung | Kombination | |
|---|---|---|---|
| Transport | 10 | Transportlagerung | 1.15*1.3*Gk + 0.83*P(t=10) + 1.15*1.3*Qk,wh |
| Montage | 11 | Montagelagerung | 1.15*1.3*Gk + 0.83*P(t=11) + 1.15*1.3*Qk,wh |
| Einbauzustand | 21 | Gabellagerung | 1.35*Gk + 0.83*P(t=21) + 1.5*Qk,wh |
| Endzustand | ∞ | Gabellagerung | 1.35*(Gk + ΔGk)+ 0.83*P(t=∞) + 1.5*Qk,s + 1.5*0.6*Qk,w |
Gemäß DIN EN 1992-1-1/NA, NDP zu 2.4.2.2 (2) ist bei der Schnittgrößenermittlung mit nichtlinearen Verfahren die Vorspannung mit γp,fav = 0.83 bzw. γp,unfav = 1.2 zu berücksichtigen.
D5 Referenzen
[1] Tillmann, M., Spannbetonbinder nach Eurocode 2, Bemessung - Erläuterungen - Checkliste, Fachvereinigung Deutscher Betonfertigteilbau e.V., 2015, 2. Auflage.
[2] König, G., Pauli, W., Nachweis der Kippstabilität von schlanken Fertigteilträgern aus Stahlbeton und Spannbeton, in: Beton- und Stahlbeton Heft 5, Heft 5 (1992).
[3] Pauli, W., Versuche zur Kippstabilität an praxisgerechten Fertigteilträgern aus Stahlbeton und Spannbeton, Darmstadt: Dissertation D 17 1990.
[4] Zedler, T., Zum Tragverhalten von Stahlbeton- und Spannbetonbalken unter Torsion, Ruhr Universität Bochum: Dissertation 2011.
[5] Wienecke, U. J., Zur wirklichkeitsnahen Berechnung von Stahlbeton- und Spannbetonstäben nach einer konsequenten Theorie II. Ordnung unter allgemeiner Belastung, Darmstadt: Dissertation D 17 1985.
[6] Röder, F.-K., Berechnung von Stahlbeton- und Spannbetonträgern nach Theorie II. Ordnung, Darmstadt: Dissertation D 17 1982.

